Artículo original
Comparación del Rectángulo de Euclides y la altura facial ideal
Objetivo: El propósito de este trabajo fue conocer la similitud estadística que existe entre la altura facial ideal propuesta en el método cefalométrico Silva (MCS) y la altura facial obtenida utilizando el rectángulo áureo (o Rectángulo de Euclides).
Método: Se utilizaron 100 imágenes cefalométricas de pacientes ortodónticos del Departamento de Ortodoncia de la Universidad Latinoamericana, campus Valle de la Ciudad de México, de ambos sexos, seleccionando aquellas que tuvieron características aptas para el trazado cefalométrico en cuestión, siendo ubicadas 85 de éstas en el programa Keynote (Apple®), realizando MCS y el trazado del Rectángulo de Euclides, cuya correlación se estableció con el coeficiente de correlación de Pearson.
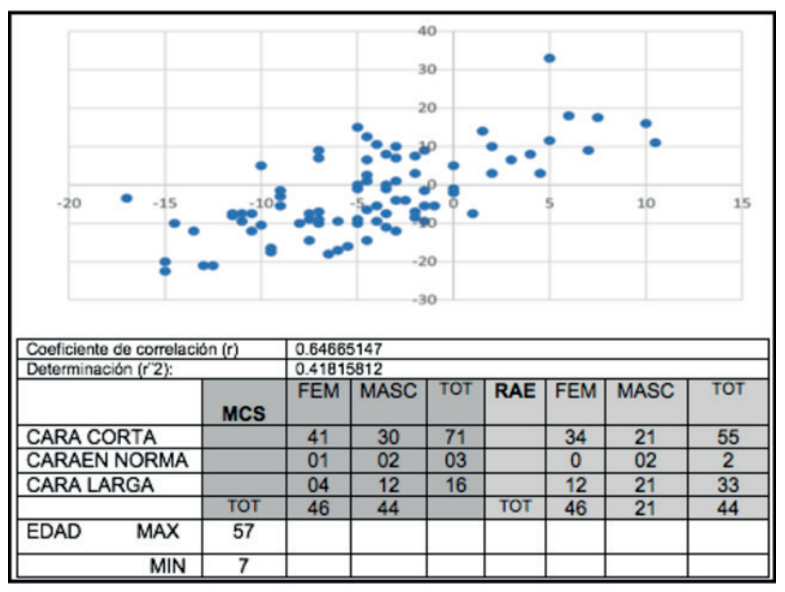
Resultados: El análisis de Pearson obtuvo un resultado de correlación importante (r)=0.69058966
Conclusiones: Los resultados estadísticos demuestran que la altura facial medida con el método cefalométrico Silva y con el rectángulo de Euclides arrojan una correlación importante pero no perfecta.
Objective: The purpose of this work was to know the statistical similarity that exists between the ideal facial height proposed in the Silva cephalometric method (SCM) and the facial height obtained using the golden rectangle (or Euclid’s Rectangle).
Method: 100 cephalometric images of orthodontic patients of the Department of Orthodontics of the Latin American University, Valle campus in Mexico City, of both sexes were used, selecting those that had characteristics suitable for the cephalometric tracing in question, 85 of these being located in the Keynote program (Apple®), performing SCM and plotting the Euclid Rectangle, the correlation of which was established with Pearson’s correlation coefficient.
Results: Pearson’s analysis obtained an important correlation result (r) = 0.69058966
Conclusions: The statistical results show that the facial height measured with the cephalometric method and the Euclidean rectangle shows an important but not perfect correlation.
Una de las relaciones de equilibrio estético más conocida es la proporción áurea, divina o Phi (Ø) en honor al escultor griego Phidias. En geometría el valor numérico de Phi es 1,618. Esta proporción, encontrada en toda la naturaleza, ha sido considerada por los ortodoncistas para establecer objetivos estéticos e incluso para la ayuda en el diagnóstico de las maloclusiones. Ricketts1 asume que el incisivo inferior es una unidad básica, el incisivo superior es dorado a la anchura del inferior, tomando ambos incisivos centrales superiores y los inferiores como una unidad, la relación entre ellos es dorada. Se ve una progresión cuando se comparan los dos incisivos centrales superiores con los cuatro incisivos superiores. Otra progresión es la anchura de los primeros premolares superiores, observando un ritmo en la oclusión ideal normal natural con el incisivo inferior como una unidad básica y Phi para los incisivos centrales superiores y, sucesivamente, se presenta la proporción con las anchuras de los incisivos laterales y éstos con los premolares. Ricketts describe una segunda serie de proporciones divinas en los dientes con las anchuras de los cuatro incisivos inferiores como valor 1,0, observando una relación de 1,618 a las puntas de los caninos superiores. Y observa la relación 2 Phi (2,618) de los cuatro incisivos inferiores a la anchura de los segundos molares superiores. Marcuschamer2 señala que, para los dientes anteriores, la suma del ancho mesiodistal desde el primer premolar superior derecho hasta el izquierdo es 1,618 veces la suma de los 6 dientes antero-inferiores (de canino a canino). Sugiere que para evaluar el sector posterior se toma como la unidad la suma de los anchos mesio-distales del primer molar permanente y los premolares, que tendrían relación áurea con la suma de los anchos mesio-distales desde el canino al segundo molar permanente superior.
Por otra parte, la aplicación de la tomografía computarizada de haz cónico (CBCT) en ortodoncia ha marcado el comienzo de una nueva era en el mejor entendimiento de la anatomía esquelética cráneo facial. Sin embargo, los análisis cefalométricos convencionales aún no son sustituidos y mucho menos descartados en el diagnóstico de las maloclusiones. El uso de análisis cefalométricos bidimensionales, tal y como los entendemos, no existen de manera tridimensional, no obstante, de ninguna manera se deben menospreciar los beneficios que representa la visualización tridimensional en el área odontológica. La medición y entendimiento de la altura y divergencia faciales se consideran información fundamental para la realización de un buen diagnóstico de la maloclusión. Sassouni3 estudió la importancia de la interacción entre las condiciones faciales verticales y horizontales. En su análisis sugiere que los planos S-N, Frankfurt, Palatal, Oclusal y Mandibular converjan en un solo punto, y clasificó la divergencia facial como divergencia neutral, hiperdivergente e hipodivergente.
Los pacientes hiperdivergentes se han asociado con músculos más pequeños y menos activos y fuerzas de mordida más débiles3 . En la literatura estas categorías se han relacionado con el crecimiento facial, sin embargo, es común confundir la altura facial con la altura de la cabeza. La cabeza se divide en tercios porque involucra la cara y el cráneo, mientras que la altura facial, es decir, la altura de la cara, no presenta tercios. También en ocasiones se confunden la divergencia facial con la altura facial, sin embargo, no siempre son coincidentes5 .
Entre los diversos métodos cefalométricos para establecer la altura facial, se utilizan medidas lineales, angulares o proporcionales. En este trabajo se utilizó el método cefalométrico propuesto por Silva5 (MCS), quien primero estima la altura facial ideal proporcional y luego la compara con la altura real del paciente para así interpretar la condición de la altura facial en tres posibilidades: cara neutra, cara larga y cara corta. Cabe mencionar que en este método la altura facial se considera independiente de la divergencia facial, ya que ésta se obtiene por el ángulo goniaco mandibular.
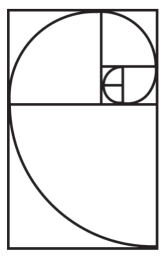
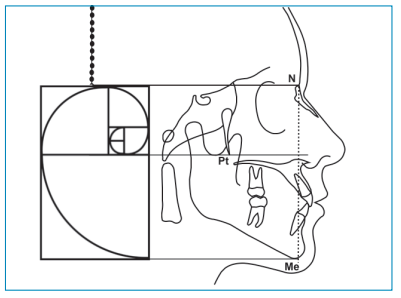
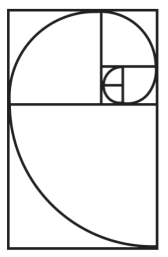
Dentro de los conocimientos de proporcionalidad, se conoce como rectángulo de Euclides o áureo un rectángulo que posee una proporcionalidad entre sus lados igual a la razón áurea, es decir, que es aquel rectángulo que al substraer la imagen del cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado. A partir de este rectángulo se puede obtener la espiral dorada que es una espiral logarítmica (Figura 1).
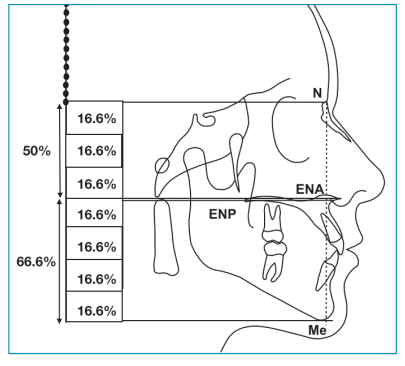
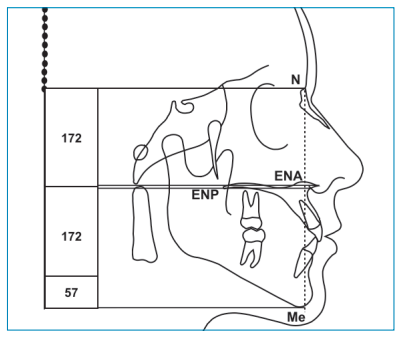
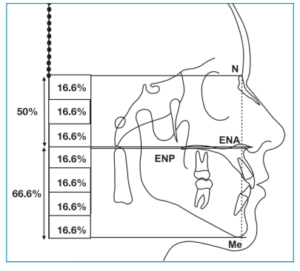
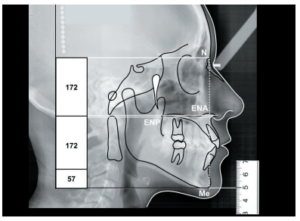
La altura facial ideal proyectada en el MCS6,7 se origina de los parámetros obtenidos en el análisis cefalométrico de Legan y Burstone8 , donde se desprende que la proporción facial se puede dividir en general en un segmento superior (N-ENA), equivalente al 50%, y un segmento inferior (ENAMe), equivalente al 66,6% aproximadamente. En el MCS el segmento facial superior se ubica con la línea horizontal de Nasion (perpendicular a la vertical verdadera) hasta la media entre las horizontales de las espinas nasales anterior y posterior, mientras que, el segmento facial inferior va desde esta línea horizontal entre las espinas nasales hacia la línea horizontal de Menton, esto por supuesto verticalmente (Figura 2).
Se utilizaron 100 imágenes con características convenientes para el trazado cefalométrico lateral ubicadas en cualquiera de los programas Keynote (Apple®) o Microsoft Power Point (Microsoft Office®) de pacientes ortodónticos de ambos sexos y de cualquier edad del Departamento de Ortodoncia de la Universidad Latinoamericana, campus Valle en la Ciudad de México D.F.
Bajo la supervisión de dos operadores se excluyeron las imágenes distorsionadas, así como aquellas en las que el paciente no tuviera posición natural de la cabeza o presentara alteraciones verticales del maxilar. 85 imágenes fueron seleccionadas y duplicadas con el fin de realizar dos trazos diferentes en cada una de ellas. El primer trazo se realizó siguiendo las indicaciones del MCS, para interpretar la condición de la altura facial (cara neutra, corta o larga). El duplicado de cada imagen se utilizó para dibujar el rectángulo de Euclides teniendo dos parámetros estandarizados, la línea horizontal de Nasion y otra línea paralela ubicada a nivel de la punta de la fosa pterigomaxilar.
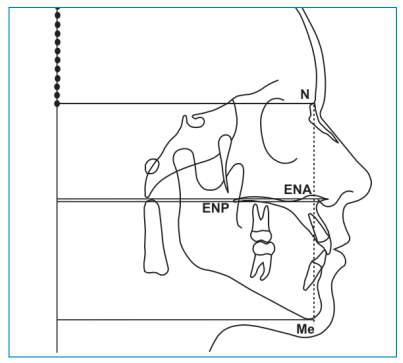
El MCS, está sustentado por dos parámetros indispensables, la posición natural de la cabeza y la vertical verdadera. Utilizando las herramientas del ordenador se interpreta la altura facial de la siguiente manera: se trazan 4 líneas horizontales paralelas y perpendiculares a la vertical verdadera, la primera ubicada en el punto Nasion, la segunda en la espina nasal anterior, la tercera en la espina nasal posterior y la cuarta en Menton (Figura 3). Posteriormente se identifica el segmento superior facial construyendo un rectángulo con las herramientas del programa ubicado entre la línea horizontal de Nasion y la media entre las dos líneas horizontales de las espinas nasales anterior y posterior, luego, dando dos clics en el rectángulo podemos ver su altura para anotarse dentro del rectángulo (Figura 4). Para identificar el segmento facial inferior, se duplica el rectángulo superior y se coloca inmediatamente por debajo del rectángulo superior, después se divide su altura entre tres y con este resultado se crea la altura del rectángulo que complementará los segmentos inferiores (Figura 5).
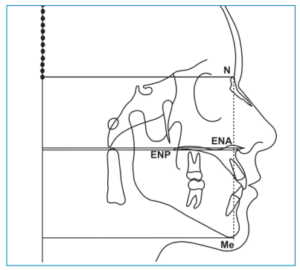
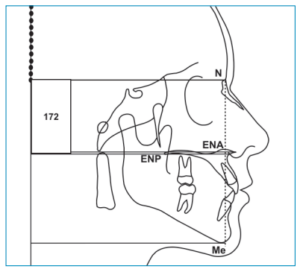
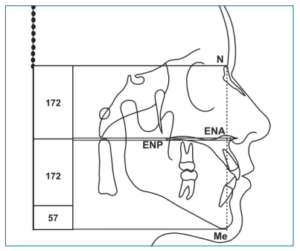
De esta manera se observa la proporción facial ideal (50%- 66,6%), es decir, la altura de los tres rectángulos representa la altura ideal facial y proyectando la base del último rectángulo inferior con una línea punteada, permite ver claramente la relación que tiene con la línea horizontal que se ubica en el punto Menton del paciente. Cuando estas dos líneas horizontales coinciden se interpreta como cara en norma o neutra. Si la línea horizontal de Menton está por debajo de la línea punteada que proyecta el rectángulo inferior, se interpreta la altura facial como cara larga, y si esta línea horizontal de Menton se encuentra por arriba de la proyección de la altura ideal se interpretará como cara corta.
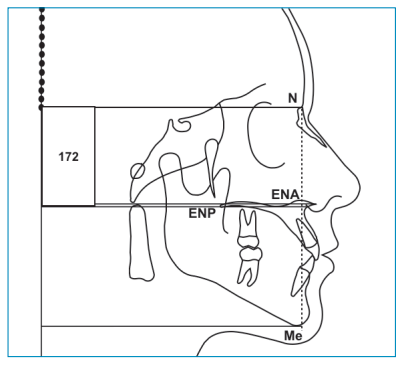
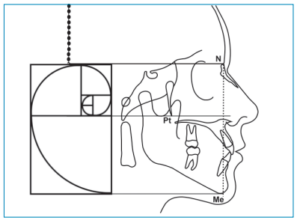
Por otro lado, encontramos que el rectángulo áureo con las proporciones propuestas por Euclides coincide con la altura facial ideal total cuando colocamos el rectángulo verticalmente y hacemos coincidir el rectángulo menor con la horizontal de Nasion y una línea horizontal perpendicular a la vertical verdadera localizada en la punta de la fosa pterigoidea (Figura 6).
Para comparar las diferencias entre los dos métodos de estimación de la altura facial ideal, en ambos métodos se clasificaron como cara neutra, corta y larga, tomando como parámetros las diferencias de posición entre la línea horizontal de Menton y la línea horizontal de la base de ambos rectángulos (de Euclides y del MCS). Se consideró cara neutra cuando las dos líneas horizontales coinciden, cara larga cuando la línea horizontal de Menton se encuentra por debajo de la línea de la base del rectángulo y cara corta cuando la línea horizontal de Menton se encuentra por encima de la línea horizontal de la base del rectángulo.
Posteriormente, con las herramientas del programa se montó una regla milimétrica calibrada para medir las diferencias entre estas dos líneas horizontales en cada paciente, anotando el sexo y la edad de cada uno para observar sus diferencias.
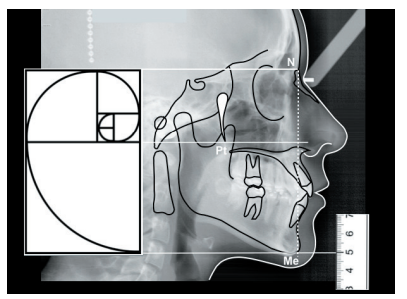
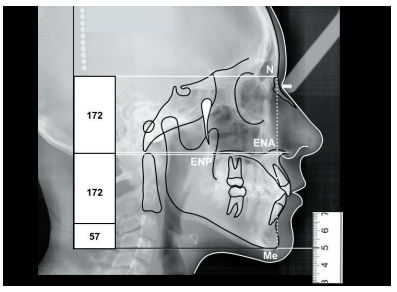
Las Figuras 7 y 8 muestran la ubicación de los dos rectángulos en una cara neutra y se observa la regla milimétrica para medir las dos líneas horizontales. La Figura 7 muestra el rectángulo de Euclides y la Figura 8 el rectángulo (creado por tres rectángulos) del MCS.
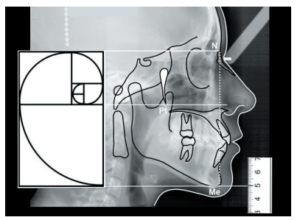
Se analizaron 85 imágenes que cumplieron con los criterios de inclusión del estudio.
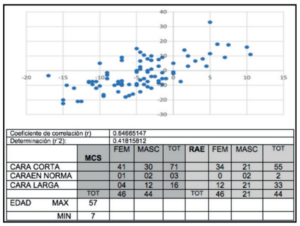
Del total de pacientes analizados, 42 fueron mujeres y 43 hombres. La edad máxima fue de 57 años mientras que la mínima fue de 7, con una media de edad de 22,2 años.
Se realizó el MCS para determinar el grupo de altura facial al que pertenecía cada paciente: cara corta, cara normal o cara larga. Posteriormente se comparó con el resultado del grupo de altura facial al ser analizado con el Rectángulo Áureo de Euclides. De las 85 imágenes analizadas, el 78,8% (67 imágenes) se clasificaron como cara corta de acuerdo al MCS (38 mujeres, 29 hombres), mientras que únicamente 61,2% (52 imágenes) pertenecieron al mismo grupo de acuerdo al RAE (32 mujeres, 20 hombres). Las imágenes clasificadas como cara normal representaron el 3,5% (3 imágenes) de acuerdo al MCS (1 mujer, 2 hombres) y 2,3% (2 imágenes) de acuerdo al RAE (2 hombres). Por último, el 17,7% (15 imágenes) de los pacientes se clasificaron como cara larga de acuerdo al MCS (3 mujeres, 12 hombres) y el 36,5% (31 imágenes) de acuerdo al RAE (10 mujeres, 21 hombres).
Con estos datos, se realizó el análisis estadístico de Coeficiente de Correlación de Pearson para determinar si existía una correlación entre ambos métodos para determinar la altura facial, donde se obtuvo un resultado de (r)=0.69058966 (Figura 9). Dicho coeficiente arroja una correlación importante entre ambos análisis, sin embargo, no es perfecta.
Comparando las medidas de la altura facial obtenidas con el Método Cefalométrico Sagital de Silva (MCS) y el Rectángulo Áureo de Euclides (RAE), alrededor del 18% de los pacientes presentaron una variación en la cual se diagnosticaron como cara corta en MCS y cara larga con el RAE. Después de analizar los resultados, se atribuyó esta diferencia a los pacientes con inclinación moderada del plano palatino, por lo que habrá que profundizar en este aspecto. Excluyendo este grupo de pacientes, el resultado del diagnóstico de la altura facial fue coincidente con ambos métodos, variando por pocos milímetros.
En los diversos análisis cefalométricos existen parámetros lineales y/o angulares utilizados para determinar la altura facial ideal, sin embargo, cuando en la interpretación diagnóstica se emplea el término divergencia facial como sinónimo de altura facial se manifiesta un error frecuente, puesto que es el ángulo goniaco de la mandíbula quien proporciona la categoría divergente y no corresponde necesariamente con la altura facial. También es común que se mencionen en la literatura los “tercios faciales”, cuando la cara (facia) no presenta tercios, si tomamos en cuenta que la cabeza se divide en cara y cráneo. En ese caso, serían tercios de la cabeza, pero las costumbres hacen leyes. De ahí que en este trabajo preferimos comparar el triángulo de Euclides con la medición vertical de Nasion a Menton para confirmar la relación proporcional, que facilita la observación de la altura facial.
Comparando las medidas obtenidas de la altura facial podemos decir que el diagnóstico vertical de la altura facial obtenida por el Método Cefalométrico Sagital es equivalente a la proporción dorada del Rectángulo de Euclides en pacientes con plano palatino en norma.
Silva Meza, Roberto
Profesor del Departamento de Ortodoncia de la Universidad Latinoamericana, campus Valle, México CDMX.
Aguilar Garza, Guillermo
Profesor del Departamento de Ortodoncia de la Universidad Latinoamericana, campus Valle, México CDMX
Indexada en / Indexed in: – IME – IBECS – LATINDEX – GOOGLE ACADÉMICO